翻转架中重型变位机的受力分析
发布时间:2017-10-26 点击次数:次
变位机是将工件回转并倾斜,使工件置于有利加工位置的变位机械,主要用于机架、机座、机壳、法兰、封头等非长形焊件的翻转变位,也可以在其上从事切割、堆焊、喷涂等作业。
在重型机械切削加工过程中,工件质量大,形状不规则,且包含个数、位置、尺寸均不相同的待加工孔,需要在变位机上完成装夹定位。
变位机需要通过旋转或翻转将工件摆放到合适的加工位置,由于工件在变位机上的装夹位置并不确定,旋转、翻转亦没有固定的顺序,因此变位机承受的载荷并不固定,随着工件以及工作位置的不同而变化。
1、两自由度变位机
某公司设计的两自由度变位机主要参数: 工件最大质量60 t,变位机工作台直径5 000 mm,夹持工件最大直径4 500 mm,工作平台翻转角度范围0 ~70°,工作平台自身旋转角度范围0 ~360°。
该变位机具有旋转和翻转两个自由度,其三维实体简化模型如图1 所示,主要由旋转工作台、翻转架和底座三大部分组成。翻转机构由两个液压马达同时驱动,通过滑动丝杠带动丝母在其轴线方向上移动,以实现翻转架的翻转运动。翻转架的上部通过外齿圈交叉滚子转盘轴承与旋转工作台连接,且为旋转夹紧机构的支座; 下部( 即腿部) 与丝母固连。变位机的翻转机构主体通过翻转轴放置在变位机基座上。翻转架既是变位机旋转工作台的基座,又是翻转机构的主体,其强度和刚度在整个变位机的结构中至关重要。
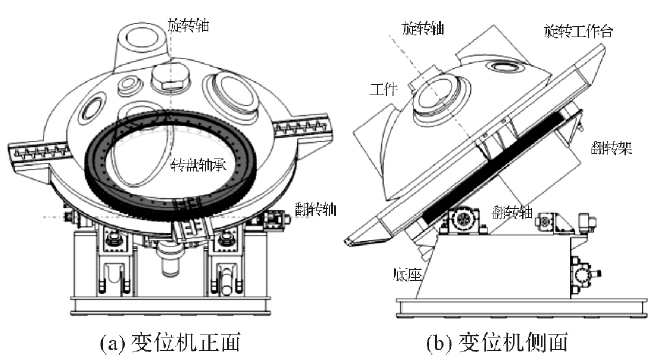
图1 重型变位机三维实体简化模型
2、变位机翻转架的静力分析
变位机为低速机械,不计惯性力,对变位机的翻转架进行静力分析,翻转架受力情况如图2所示。翻转架受到其自身以及所有翻转部件(包括工件)的重力G 作用,在翻转轴C 处受到支座的反作用力FCx和FCy,丝母B 处受到沿着其轴线方向的作用力F。
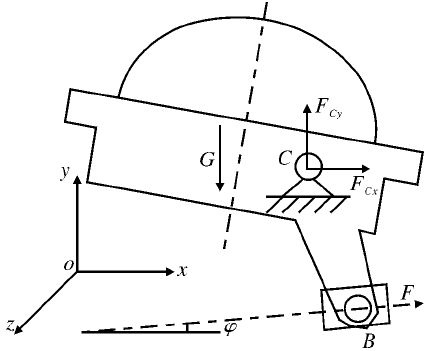
图2 翻转架受力分析图
在给定变位机翻转角度的情况下,翻转部件的重心与翻转轴的相对位置以及产生的绕翻转轴的扭矩是确定的; 由于工件偏心,其重心与翻转轴的相对位置并不确定,工件重力对翻转轴产生的扭矩随着工件重心在工作台平面上位置的变化而不断变化。所以力矩M 分为由翻转部件产生的不变扭矩M1和由工件产生的可变扭矩M2两部分。如图3 所示,s1表示翻转部件重心位置,s2表示工件重心位置,s1和s2与翻转轴C 的相对位置分别用e1、h1、e2、h2来表示。
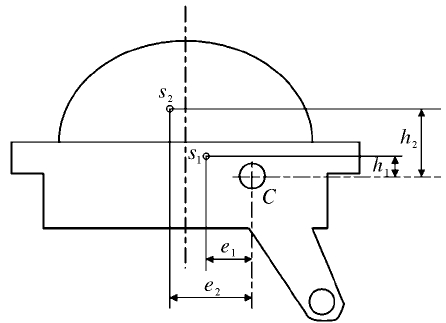
图3 翻转部件重心位置图
翻转部件重心位置与高度确定,而工件重心与翻转轴之间的距离e2随工件在工作台上的摆放位置不同而变化。在变位机旋转轴线所在的与工作台面平行的平面上建立坐标系xoy,如图4所示。x 轴与翻转轴平行,工件偏心半径为e,且旋转轴线在坐标平面的投影点与翻转轴的距离用l 表示,工件重心s2在工作台上的位置用表示。工件的任意摆放位置均可以用0° ~ 360°之间的唯一β 值表示出来。
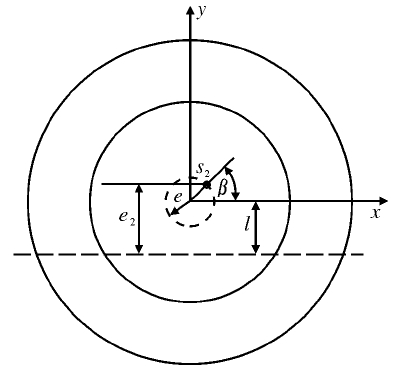
图4 工件重心位置
根据受力平衡条件可以,得出F、FCx、FCy分别为
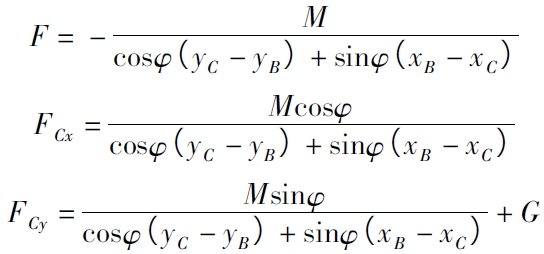
式中,φ 为丝杠与水平面的夹角; ( xB、yB) 为丝母B 点的坐标; xC、yC为翻转轴C 点的坐标; M为重力G 产生的相对于翻转轴C 的扭矩。
将F、FCx、FCy反向之后,便可以得到丝杠所受轴向力以及翻转轴的受力情况。
在变位机的任意翻转角度,翻转部件的重力产生的绕翻转轴的扭矩计算公式为
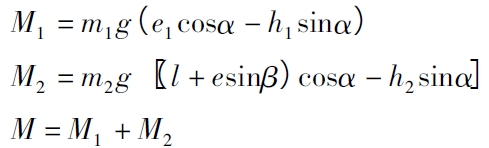
从扭矩计算公式中可以看出,对于给定的翻转角度α,当β = π/2 时,扭矩出现最大值,当β =3π/2 时,扭矩出现最小值。因此,分别考虑工件处于这两个位置时,丝母轴线方向的作用力F 以及翻转轴处支反力FCx、FCy随翻转角度α 的变化情况。
3、翻转机构的静力分析结果
在Matlab 软件中编程计算,分别得出当β =π/2 和β = 3π/2 时,丝母轴线方向作用力F、翻转轴处支反力FCx、FCy随翻转角度α 的变化情况。
(1) 当β = π/2 时,丝母轴线方向作用力F随翻转角度的变化曲线如图5 所示。从图中可以看出,水平位置时,F 为- 1. 270 × 106 N,丝杠受拉; 随着翻转角度的增大,丝杠拉力逐渐减小,直至翻转角度为35. 66° 时丝杠受力为零;之后,丝杠受压,且压力大小随着翻转角度的增大而增大,直到翻转角度为70° 时,压力最大,为1. 223 × 106 N。
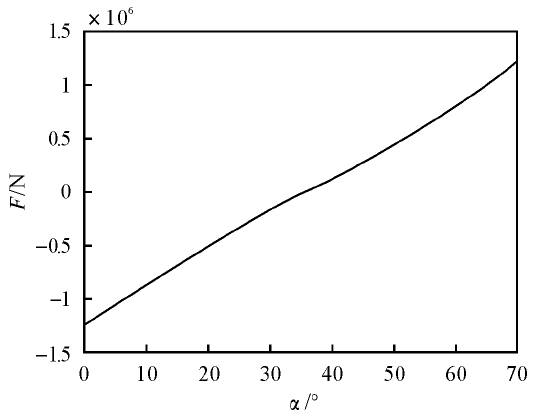
图5 F-曲线
翻转轴C 处x 方向支反力FCx随翻转角度α变化曲线如图6 所示。从图中可以看出,水平位置时,FCx的值最大,为1. 270 × 106 N; 随着翻转角度的增大,FCx数值减小,直到为零之后又反向增加,翻转70°时,FCx的值为1. 2228 × 106N,方向是沿x 的负方向。
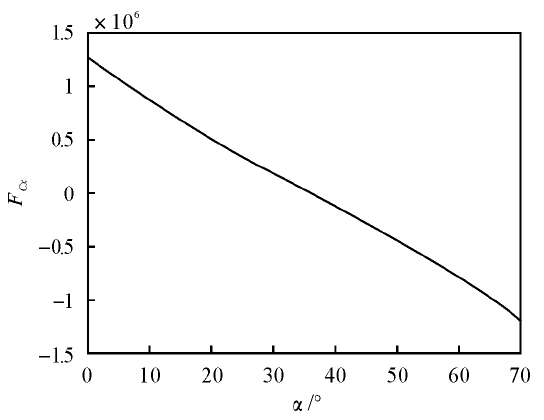
图6 FCx - α 曲线
翻转轴C 处y 方向支反力FCy随翻转角度α变化曲线如图7 所示。从图中可以看出,FCy的最大值为1. 1344 × 106 N,最小值为1. 052 4 ×106 N,相差不多,说明随着翻转角度的增加,翻转轴处y 方向的支反力变化不大。
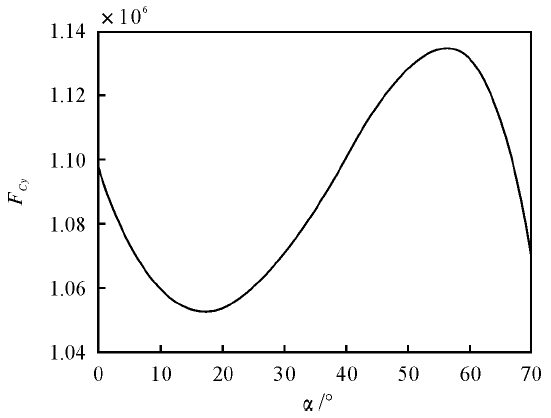
图7 FCy - α 曲线
(2) 当β = 3π/2 时,F、FCx、FCy随翻转角度α 的变化曲线与β = π/2 时相比,曲线变化趋势一致,只是对应于同一翻转角度时的数值不同,不再给出图示。具体的比较见表1。
对比F、FCx、FCy在β = π/2 和β = 3π/2 两种情况下的极值大小可以看出,当变位机处于水平位置且β = π/2 时,丝杠承受最大拉力,为1. 270 × 106 N,此时x 正方向的支座反力最大;当变位机翻转70°且β = 3π/2 时,丝杠承受最大压力,为1. 231 × 106 N,此时x 负方向的支座反力最大; y 方向的支座反力的最大值与最小值相差不大,且在两种情况下更是相差甚微。
综合上述两种情况,可以得出变位机受力的两个极限位置: 变位机水平位置且β = π/2,变位机翻转70°且β = 3π/2。本文以变位机水平位置且β = π/2 极限位置时对翻转架进行有限元分析。
4、翻转架水平位置时有限元分析
有限元分析结果的可信度直接受分析模型、载荷处理、约束条件和实际工程结构力学特性符合程度的影响,建立有限元分析模型时既要如实反映实际结构的重要力学特性,又要尽量采用较少的单元和简单的单元形态,以保证较高的计算精度及缩小解题规模。
利用SolidWorks 软件建立翻转架的三维模型,在COSMOS Works 中,建立翻转架水平位置时的分析模型如图8 所示。翻转架材料选用普通碳钢,水平位置时,受到自身重力、工件以及翻转部件的重力作用,在与丝杠连接的位置受到沿着丝杠轴线方向的作用力635 000 N,为了将丝杠轴线方向的作用力准确地施加到翻转架模型上,首先建立沿丝杠轴线方向的基准轴,以便加载时准确确定载荷方向。翻转轴通过轴承坐落在机座上,在翻转轴与轴承的接触面上定义铰链约束。

图8 翻转架水平位置有限元分析模型
划分实体网格进行分析之后,利用软件的后处理功能,输出翻转架在水平位置时的应力云图和位移云图分别如图9、10 所示。
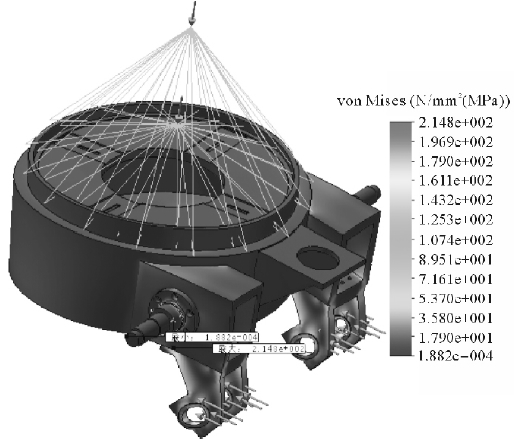
图9 翻转架水平位置应力云图
计算结果应力单位为MPa,位移单位为mm,变形比例为554. 4。图中的Von Mises 应力是按第四强度理论计算的第四相当应力,所显示的URES 位移是各点的总位移。
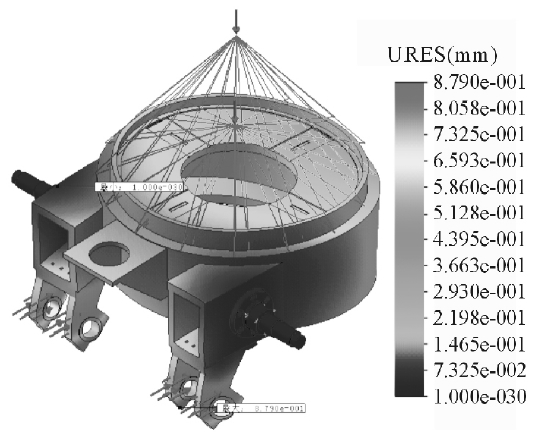
图10 翻转架水平位置合位移云图
从图中可以看出,最大应力为214. 8 MPa,发生在翻转架的腿部。最大位移亦发生在翻转架的腿部,其值为0. 879 mm。
同时可以利用COSMOS Works 的后处理功能测得翻转轴处的支反力,检测结果见表2。
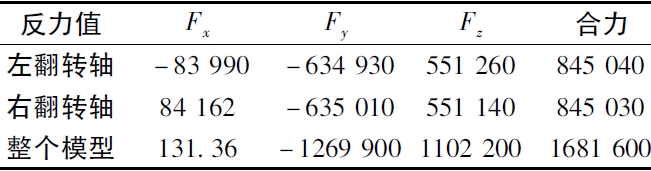
表2 翻转架水平位置时支反力检测结果
翻转架翻转69°时,不仅受到自身重力、工件以及旋转部件的重力作用、丝杠轴线方向的作用力,还要考虑加工21°孔时的切削力。最终从翻转架在水平位置和翻转69°两种工况下的分析可以看出: 翻转架的应力分布不均匀,应力较大的位置集中分布在翻转架的腿部,应力最大值出现在翻转架的腿与翻转架的连接部位,应力值为214. 8 MPa,小于普通碳钢的屈服强度值220. 59MPa,翻转架的强度满足要求; 翻转架变形较大的位置亦发生在翻转架的腿部,最大位移值为0. 879 mm。
5、结论
(1) 通过对变位机翻转架进行静力分析,得出翻转架受力极限位置: 变位机水平位置且β=π/2; 变位机翻转70°且β=3π/2。
(2) 通过对翻转架受力极限位置进行有限元分析得出: 翻转架的腿部是翻转架最关键的部位,变位机工作过程中受力状态不是很好,可以选用屈服强度较大的合金钢来制造翻转架的腿部,以提高翻转架的整体强度。还可以从优化翻转架腿部结构的方面考虑,使翻转架更加安全可靠。
(3) 该研究成果指导的变位机系统的设计开发,目前变位机已成功投入使用。
友情提示:
您只要致电:021-60641703 021-60766769 (0)15216837090(张经理)
我们可以解答汽车变速器实训台, 汽车教学设备, 汽车变速器拆装实训台相关疑问!
我们可以帮您推荐符合您要求的汽车变速器实训台, 汽车教学设备, 汽车变速器拆装实训台相关产品!。
在重型机械切削加工过程中,工件质量大,形状不规则,且包含个数、位置、尺寸均不相同的待加工孔,需要在变位机上完成装夹定位。
变位机需要通过旋转或翻转将工件摆放到合适的加工位置,由于工件在变位机上的装夹位置并不确定,旋转、翻转亦没有固定的顺序,因此变位机承受的载荷并不固定,随着工件以及工作位置的不同而变化。
1、两自由度变位机
某公司设计的两自由度变位机主要参数: 工件最大质量60 t,变位机工作台直径5 000 mm,夹持工件最大直径4 500 mm,工作平台翻转角度范围0 ~70°,工作平台自身旋转角度范围0 ~360°。
该变位机具有旋转和翻转两个自由度,其三维实体简化模型如图1 所示,主要由旋转工作台、翻转架和底座三大部分组成。翻转机构由两个液压马达同时驱动,通过滑动丝杠带动丝母在其轴线方向上移动,以实现翻转架的翻转运动。翻转架的上部通过外齿圈交叉滚子转盘轴承与旋转工作台连接,且为旋转夹紧机构的支座; 下部( 即腿部) 与丝母固连。变位机的翻转机构主体通过翻转轴放置在变位机基座上。翻转架既是变位机旋转工作台的基座,又是翻转机构的主体,其强度和刚度在整个变位机的结构中至关重要。

图1 重型变位机三维实体简化模型
2、变位机翻转架的静力分析
变位机为低速机械,不计惯性力,对变位机的翻转架进行静力分析,翻转架受力情况如图2所示。翻转架受到其自身以及所有翻转部件(包括工件)的重力G 作用,在翻转轴C 处受到支座的反作用力FCx和FCy,丝母B 处受到沿着其轴线方向的作用力F。

图2 翻转架受力分析图
在给定变位机翻转角度的情况下,翻转部件的重心与翻转轴的相对位置以及产生的绕翻转轴的扭矩是确定的; 由于工件偏心,其重心与翻转轴的相对位置并不确定,工件重力对翻转轴产生的扭矩随着工件重心在工作台平面上位置的变化而不断变化。所以力矩M 分为由翻转部件产生的不变扭矩M1和由工件产生的可变扭矩M2两部分。如图3 所示,s1表示翻转部件重心位置,s2表示工件重心位置,s1和s2与翻转轴C 的相对位置分别用e1、h1、e2、h2来表示。

图3 翻转部件重心位置图
翻转部件重心位置与高度确定,而工件重心与翻转轴之间的距离e2随工件在工作台上的摆放位置不同而变化。在变位机旋转轴线所在的与工作台面平行的平面上建立坐标系xoy,如图4所示。x 轴与翻转轴平行,工件偏心半径为e,且旋转轴线在坐标平面的投影点与翻转轴的距离用l 表示,工件重心s2在工作台上的位置用表示。工件的任意摆放位置均可以用0° ~ 360°之间的唯一β 值表示出来。

图4 工件重心位置
根据受力平衡条件可以,得出F、FCx、FCy分别为
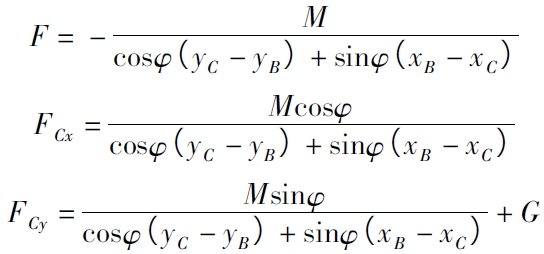
式中,φ 为丝杠与水平面的夹角; ( xB、yB) 为丝母B 点的坐标; xC、yC为翻转轴C 点的坐标; M为重力G 产生的相对于翻转轴C 的扭矩。
将F、FCx、FCy反向之后,便可以得到丝杠所受轴向力以及翻转轴的受力情况。
在变位机的任意翻转角度,翻转部件的重力产生的绕翻转轴的扭矩计算公式为
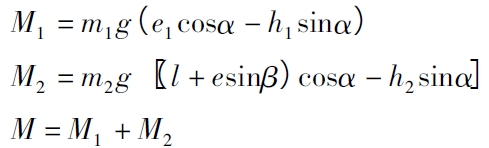
从扭矩计算公式中可以看出,对于给定的翻转角度α,当β = π/2 时,扭矩出现最大值,当β =3π/2 时,扭矩出现最小值。因此,分别考虑工件处于这两个位置时,丝母轴线方向的作用力F 以及翻转轴处支反力FCx、FCy随翻转角度α 的变化情况。
3、翻转机构的静力分析结果
在Matlab 软件中编程计算,分别得出当β =π/2 和β = 3π/2 时,丝母轴线方向作用力F、翻转轴处支反力FCx、FCy随翻转角度α 的变化情况。
(1) 当β = π/2 时,丝母轴线方向作用力F随翻转角度的变化曲线如图5 所示。从图中可以看出,水平位置时,F 为- 1. 270 × 106 N,丝杠受拉; 随着翻转角度的增大,丝杠拉力逐渐减小,直至翻转角度为35. 66° 时丝杠受力为零;之后,丝杠受压,且压力大小随着翻转角度的增大而增大,直到翻转角度为70° 时,压力最大,为1. 223 × 106 N。

图5 F-曲线
翻转轴C 处x 方向支反力FCx随翻转角度α变化曲线如图6 所示。从图中可以看出,水平位置时,FCx的值最大,为1. 270 × 106 N; 随着翻转角度的增大,FCx数值减小,直到为零之后又反向增加,翻转70°时,FCx的值为1. 2228 × 106N,方向是沿x 的负方向。

图6 FCx - α 曲线
翻转轴C 处y 方向支反力FCy随翻转角度α变化曲线如图7 所示。从图中可以看出,FCy的最大值为1. 1344 × 106 N,最小值为1. 052 4 ×106 N,相差不多,说明随着翻转角度的增加,翻转轴处y 方向的支反力变化不大。

图7 FCy - α 曲线
(2) 当β = 3π/2 时,F、FCx、FCy随翻转角度α 的变化曲线与β = π/2 时相比,曲线变化趋势一致,只是对应于同一翻转角度时的数值不同,不再给出图示。具体的比较见表1。
对比F、FCx、FCy在β = π/2 和β = 3π/2 两种情况下的极值大小可以看出,当变位机处于水平位置且β = π/2 时,丝杠承受最大拉力,为1. 270 × 106 N,此时x 正方向的支座反力最大;当变位机翻转70°且β = 3π/2 时,丝杠承受最大压力,为1. 231 × 106 N,此时x 负方向的支座反力最大; y 方向的支座反力的最大值与最小值相差不大,且在两种情况下更是相差甚微。
综合上述两种情况,可以得出变位机受力的两个极限位置: 变位机水平位置且β = π/2,变位机翻转70°且β = 3π/2。本文以变位机水平位置且β = π/2 极限位置时对翻转架进行有限元分析。
4、翻转架水平位置时有限元分析
有限元分析结果的可信度直接受分析模型、载荷处理、约束条件和实际工程结构力学特性符合程度的影响,建立有限元分析模型时既要如实反映实际结构的重要力学特性,又要尽量采用较少的单元和简单的单元形态,以保证较高的计算精度及缩小解题规模。
利用SolidWorks 软件建立翻转架的三维模型,在COSMOS Works 中,建立翻转架水平位置时的分析模型如图8 所示。翻转架材料选用普通碳钢,水平位置时,受到自身重力、工件以及翻转部件的重力作用,在与丝杠连接的位置受到沿着丝杠轴线方向的作用力635 000 N,为了将丝杠轴线方向的作用力准确地施加到翻转架模型上,首先建立沿丝杠轴线方向的基准轴,以便加载时准确确定载荷方向。翻转轴通过轴承坐落在机座上,在翻转轴与轴承的接触面上定义铰链约束。

图8 翻转架水平位置有限元分析模型
划分实体网格进行分析之后,利用软件的后处理功能,输出翻转架在水平位置时的应力云图和位移云图分别如图9、10 所示。

图9 翻转架水平位置应力云图
计算结果应力单位为MPa,位移单位为mm,变形比例为554. 4。图中的Von Mises 应力是按第四强度理论计算的第四相当应力,所显示的URES 位移是各点的总位移。

图10 翻转架水平位置合位移云图
从图中可以看出,最大应力为214. 8 MPa,发生在翻转架的腿部。最大位移亦发生在翻转架的腿部,其值为0. 879 mm。
同时可以利用COSMOS Works 的后处理功能测得翻转轴处的支反力,检测结果见表2。

表2 翻转架水平位置时支反力检测结果
翻转架翻转69°时,不仅受到自身重力、工件以及旋转部件的重力作用、丝杠轴线方向的作用力,还要考虑加工21°孔时的切削力。最终从翻转架在水平位置和翻转69°两种工况下的分析可以看出: 翻转架的应力分布不均匀,应力较大的位置集中分布在翻转架的腿部,应力最大值出现在翻转架的腿与翻转架的连接部位,应力值为214. 8 MPa,小于普通碳钢的屈服强度值220. 59MPa,翻转架的强度满足要求; 翻转架变形较大的位置亦发生在翻转架的腿部,最大位移值为0. 879 mm。
5、结论
(1) 通过对变位机翻转架进行静力分析,得出翻转架受力极限位置: 变位机水平位置且β=π/2; 变位机翻转70°且β=3π/2。
(2) 通过对翻转架受力极限位置进行有限元分析得出: 翻转架的腿部是翻转架最关键的部位,变位机工作过程中受力状态不是很好,可以选用屈服强度较大的合金钢来制造翻转架的腿部,以提高翻转架的整体强度。还可以从优化翻转架腿部结构的方面考虑,使翻转架更加安全可靠。
(3) 该研究成果指导的变位机系统的设计开发,目前变位机已成功投入使用。
您只要致电:021-60641703 021-60766769 (0)15216837090(张经理)
我们可以解答汽车变速器实训台, 汽车教学设备, 汽车变速器拆装实训台相关疑问!
我们可以帮您推荐符合您要求的汽车变速器实训台, 汽车教学设备, 汽车变速器拆装实训台相关产品!。


